모집단에서 표본을 추출하면 이로부터 모집단의 관심 모수에 관한 점추정값을 구하고, 이, 점추정값의 정밀성 정도를 평가하기 위해 표준오차(10장)를 계산하게 된다. 사실 표준오차 값 그 자체는 대부분의 연구자들에게 그다지 유용하지 않다. 하지만 이 정밀성 척도는 모집단의 모수에 관한 구간추정을 하는 데 매우 효과적으로 사용된다. 모수를 추정하기 위해 주로 사용되는 구간추정 방법은 표본에서 얻어진 통계량의 이론적인 확률분포에 근거해 신뢰구간(confidence interval; CI)을 구하는 방법이다. 일반적으로 신뢰구간이란 점추정값을 중심으로 좌우로 표준오차의 몇 배수만큼 떨어진 값들을 계산한 뒤) 이를 구간 형태로 표현한 것이다. 이렇게 계산된 좌우 두 개의 구간 끝 값을 신뢰한계 (confidence limits) 라 하마 보통의 경우 신뢰구간은 두 신뢰한계를 양 괄호 안에 콤마로 구분하여 표현한다.
모평균에 대한 신뢰구간(confidence interval for the population mean)
정규분포를 이용하는 방법
앞에서 언급한 것처럼 만일 모집단으로부터 동일 크기의 표본을 반복적으로 추출한 뒤, 각표본으로부터 표본평균을 계산한다면, 그리고 해당 표본 수가 크다면, 이 표본평균들은 정규분포에 따르게 된다. 따라서 모평균에 대한 신뢰구간을 구하기 위해 표본평균을 사용하는 경우에는 이 정규분포의 특성을 이용하면 된다. 즉, 이 표본평균들 중 95%는 모평균을 중심으로 좌우 1.96배의 (표본평균들의) 표준편차(SD) 내에 존재하게 될 것이다. 이 표본평균들의 표준편차를 ‘표본평균의 표준오차(SEM) ’라 한다 (10장). 모집단으로부터 표본을 한 번만 추출하는 경우에는 SEM = (J/&i와 같고, 따라서 모평균에 대한 95% 신뢰구간은 다음과 같이 계산된다.

그런데 일반적으로 모표준편차는 알 수 없으므로 (만일 표본 수가 충분히 크다면) 다음과 같이 신뢰구간을 근사적으로 계산하게 된다.

만일 위와 같은 실험을 여러 번 반복해서 매번 이러한 구간을 구한다면, 이 구간들 중 95%는 모수를 포함하고 있을 것이다. 현재 얻어진 자료로부터 계산된 모평균에 대한 95% 신뢰구간은 바로 이 신뢰구간들 중 하나라고 간주하면 된다. 보통의 경우, 이 신뢰구간은 ‘해당 구간 내에 실제 모평균이 존재할 확률(즉, 해당 신뢰구간이 모평균을 포함하고 있을 확률)이 95%라고 믿을 수 있는 구간’으로 해석한다. 사실 엄밀하게 보면 틀린 말이긴 하지만 (왜냐하면 모평균은 변하지 않는, 따라서, 어떤 구간 내에 있을 수도 혹은 없을 수도 있는 값이 아니기 때문이다.) 이해하기 쉽기 때문에 일단은 우리도 이와 같이 해석하자.
t-분포를 이용하는 방법
정확하게 말하자면 신뢰구간을 구할 때 모분산 (T2을 알고 있는 경우에만 정규분포를 사용해야 한다. 모분산을 모른다면, 표본 수가 충분히 큰 경우에 한해서 중심극한정리를 적용해 정규분포를 사용할 수 있다. 만일 표본 수가 적다면 모집단 자료가 정규분포를 한다는 조건 하에만 표본평균이 정규분포에 따르게 된다. 그렇다면 모분산도 모르고 자료가 정규분포를 하지도 않는다면 (혹은 이를 평가할 수 있을 정도로 표본 수가 크지 않다면) 어떻게 해야하는가? 모분산을 모르기 때문에 T2에 대한 추정값으로 s2을 사용할 것이고 이 경우 표본평균은 t분포에 따르게 되며, 따라서 모평균에 대한 95% 신뢰구간은 다음과 같이 계산된다.


즉 왼쪽 식으로 추정한다. 여기서 to.05는 자유도가 n - 1 인 t분포에서 양쪽 꼬리확률이 0.05인 경우에 해당하는 백분위수(percentile)이다. 일반적으로 t분포를 이용한 신뢰구간은 정규분포에 기초한 신뢰구간보다 약간 넓게 된다. 그 이유는 신뢰구간을 계산할 때 모표준편차를 추정해야 하기 때문에, 이로 인해 발생하는 추가적인 불확실성이 반영되기 때문이며, 또한 표본 수가 적기 때문이기도 하다. 하지만 표본 수가 크면 두 분포의 차이는 거의 없게 된다. 따라서 이제부터는 모평균에 대한 신뢰구간을 구할 때 표본수 크기에 상관없이 항상 t-분포를 사용하기로 한다. 또한. 이제부터, 특별한 언급이 없는 한 신뢰구간을 말할 때에는 95% 신뢰구간을 의미하는 것으로 한다. 물론 다른 신뢰구간, 예를 들면 모평균에 대한 99% 신뢰구간 등을 구할 수도 있다. 이 경우에는 양쪽 꼬리확률이 0.05인 경우에 해당하는 t-분포표의 값을 표준오차에 곱하는 대신, 양쪽 꼬리확률이 0.01에 해당하는 t-값을 곱해주면 된다. 99% 신뢰구간은 95% 신뢰구간에 비해 상대적으로 실제 모평균을 포함할 것이라고 믿을 수 있는 신뢰도가 더 커지기 때문에, 당연히 99% 신뢰구간의 폭이 더 넓어지게 된다.
모비율에 대한 신뢰구간(confidence interval for the population proportion)
표본비율의 표본추출 분포는 이항분포이다 (8장). 그러나 표본 수 n 이 충분히 크다면 (얻어진)
표본비율의 표본추출 분포(sampling distribution of the proportion) 26)는 근사적으로 평균이 군인 정규분포에 따르게 된다. 모비율 T를 추정하기 위해 표본비율 p = r/n을 사용한다면 [여기서 r은 대상자들 중 관심사건(정공’)이 관찰된 사람들의 수이다.] 해당 표본비율의 표준오차 추정값은 다음과 같다.
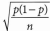
따라서 모비율에 대한 95% 신뢰구간은 다음과 같이 추정될 수 있다.

표본 수가 적은 경우(일반적으로 np나 n(l - p) 값이 5보다 작은 경우)에는 이항 분포를 사용한 정확 신뢰구간(exact confidence interval)을 계산할 수도 있다. R1) 참고로 만일 p가 비율이 아닌 백분율로 표현된 수치이면 위 식의 (1 -p)를 (100 — p)로 바꿔주면 된다.
신뢰구간의 해석
신뢰구간을 해석할 때에는 다음과 같은 사항들을 고려해야 한다.
• 산뢰구간이 얼마나 넓은가? 신뢰구간이 넓다는 것은 얻어진 점추정값이 정밀한 값이 아니라는 의미이며, 신뢰구간이 좁다는 것은 정밀하다는 의미이다. 신뢰구간의 너비를 결정하는 것은 표준오차의 크기이며, 따라서 신뢰구간의 너비는 표본 수에 의해 영향을 받게 된다. 연속형 변수의 경우에는 이에 더불어 자료의 변동량도 영향을 미치게 된다. 따라서 자료의 변동이 심한 소규모 연구는 작은 변동을 가진 대규모 연구에 비해 상대적으로 더 넓은 신뢰구간을 제공하게 된다.
• 신뢰구간으로부터 어떤 임상적/보건학적 의미를 도출할 수 있는가? 신뢰구간이 임상적/보건학적으로 중요한 의미를 가지고 있는지를 평가하기 위해서는 해당 신뢰구간의 상한 및 하한을 사용한다.
• 산뢰구간이 특별히 관심 있는 값을 포함하고 있는가? 모수가 어떤 값일 것이라는 가설을 평가하기 위해서는 해당값이 신뢰구간 내에 포함되는지를 검토하면 된다. 만일 신뢰구간이 이 값을 포함하고 있으면 모수는 그 값일 가능성 이 높다. (95% 신뢰구간 하에서 모수가 그 값이 아닐 가능성은 기껏해야 5% 정도이다.) 만일 신뢰구간이 이 값을 포함하고 있지 않다면 모수는 그 값이 아닐 기능성이 높다. (95% 신뢰구간 하에서 모수가 그 값일 가능성은 기껏해야 5% 정도이다.)
자유도(degree of freedom, df)
통계학을 공부하다 보면 ‘자유도’라는 용어를 자주 접하게 된다. 일반적으로 자유도는 (표본수 - 제약조건의 수)를 의미한다; 여기서 제약조건의 수는 추정이 필요한 모수의 수라고 봐도 좋다. 간단한 예를 들어보자. 합이 T가 되는 수 3 개가 있다고 가정하자. 합이 T라는 제약조건 하에서 이들 3 개의 수 중 2개는 어떤 값도 ‘자유롭게’ 취할 수 있지만, 나머지 하나는 (수 3 개의 합이 T가 되어야 한다는 제약조건 때문에) 다른 값을 취할 수가 없다. 따라서 수의 합이 T라는 제약조건 하에서는 이들 수 3 개의 자유도는 2가 된다. 이와 마찬가지로 표본분산

의 자유도는 표본 수 - 1 (즉, n -1)이다. 왜냐하면 표본분산 s2을 계산하기 위해서는 모평균에 관한 추정값인 표본평균(x)을 미리 계산해야만 하며, 따라서 표본평균이 이미 계산된 경우 표본분산의 자유 도는 자료의 수 -1이기 때문이다.
봇스트랩핑(bootstrapping)과 잭나이핑 Jacknifing)
붓스트랩핑과 잭나이핑은 모수 및 모수의 신뢰구간에 대한 불편추정값(unbiased estimate)을계산하는 데 사용되는 통계적 방법들 중 하나이다. 붓스트랩핑이란 (예를 들면 표본평균에 관한 정규분포 가정 등과 같이) 추정값에 대한 표본추출 분포를 가정하지 않고, 고도의 컴퓨터모의실험 (simulation)을 통해 모수에 대한 신뢰구간을 유도하는 통계적 방법이다. 먼저 원자료 표본으로부터 대규모(보통 1,000 개 이상)의 표본들을 추출한다. 이때 각 표본의 크기는 원자료의 표본 수와 동일한 크기로 하며, 표본추출은 복원추출(with replacement)로 실시한다. 복원추출이란 이미 추출된 사람도 다시 표본추출 대상으로 포함시켜 재차 표본으로 추출될 수 있도록 하는 것을 말하며, 따라서 동일한 사람이 한 표본 내에 여러 번 포함될 수 있다. 붓스트랩핑은 이와 같이 추출된 대규모 표본들 각각에 대해서 관심 모수에 관한 추정값을 계산하고, 이 추정값들 분포의 변동을 이용해 모수에 관한 신뢰구간을 예측하는 방법이다. (예를 들면, 95% 신뢰구간을 구하고자 한다면 추정값들의 2.5 번째 백분위수와 97.5 번째 백분위수를 95% 붓스트랩 신뢰구간으로 정의한다.) 잭나이핑은 붓스트랩핑과 유사한 기법이긴 하지만, 원자료 표본을 이용해 표본을 추출하는 것이 아니라, 표본 크기 n 인 원자료로부터 관찰값 하나를 제외한 후, 남아있는 n-1 개의 관찰값들을 사용해 관심 모수에 관한 추정값을 계산한다는 점에서 붓스트랩핑과 다르다. 잭나이핑은 자료 내 n 개 관찰값들 각각을 돌아가면서 제외하고 n - 1 개의 관찰값들만으로 모수를 추정하는 작업을 반복적으로 실시하여 모수에 대한 추정값들 n 개를 계산하는 방법이다. 붓스트랩핑과 마찬가지로 이들 n 개 추정값들의 변동을 사용해 관심 모수에 대한 잭나이핑 신뢰구간을 구한다.
붓스트랩핑과 잭나이핑은 예후지수를 생성하고 그 타당도를 평가하는 데 사용되기도 한다.
'보건학 관련' 카테고리의 다른 글
| 통계학13(연구설계2) (2) | 2024.01.31 |
|---|---|
| 통계학12(연구설계1) (2) | 2024.01.31 |
| 통계학9(자료의 변환) (3) | 2024.01.31 |
| 통계학5(자료의 기술, 평균적인 값) (1) | 2024.01.30 |
| 통계학7(정규분포) (1) | 2024.01.30 |


